Tour de Elastiknn

Introduction

This article is a tour through Elastiknn’s implementation and underlying concepts in fairly thorough detail. The best way to get more detail is to explore and contribute to the project.

This article should convey that Elastiknn is just a combination of a few simple concepts, with a couple interesting optimizations for improved performance.

We assume some familiarity with nearest neighbor search (i.e., vector search)¹ and Elasticsearch and Lucene.² Some knowledge of Locality Sensitive Hashing³ is helpful but not strictly necessary.

We will not directly cover the Elastiknn API. If that’s of interest, please see the API docs and the tutorial for Multimodal Search on the Amazon Products Dataset.

The tour is structured as follows:

1. Elastiknn’s features at a high level.
2. Some software engineering details.
3. Locality Sensitive Hashing (LSH) in enough detail to understand its use in Elastiknn.
4. The specific implementation of LSH indexing and querying in Elastiknn.
5. Some interesting open questions.

What does Elastiknn do?

In short, Elastiknn is an Elasticsearch plugin for exact and approximate nearest neighbor search. The name is a combination of Elastic and KNN (K-Nearest Neighbors).

The full list of features (copied from the home page) is as follows:

• Datatypes to efficiently store dense and sparse numerical vectors in Elasticsearch documents, including multiple vectors per document.
• Exact nearest neighbor queries for five similarity functions: L1, L2, Cosine, Jaccard, and Hamming.
• Approximate queries using Locality Sensitive Hashing for L2, Cosine, Jaccard, and Hamming similarity.
• Integration of nearest neighbor queries with standard Elasticsearch queries.
• Incremental index updates: start with any number of vectors and incrementally create/update/delete more without ever re-building the entire index.
• Implementation based on standard Elasticsearch and Lucene primitives, entirely in the JVM. Indexing and querying scale horizontally with Elasticsearch.

The API is embedded into the Elasticsearch JSON-over-HTTP API – see the API docs.

There are language-specific HTTP clients for Python, Java, and Scala. There are also Java libraries exposing the LSH models and Lucene abstractions for standalone use. The clients and libraries are documented on the Libraries page.

Software Background

Elasticsearch Plugins

Elasticsearch’s documentation for plugin authors is pretty minimal – it’s definitely an expert-level feature. However, there are plenty of examples to learn from. Most of the Elasticsearch datatypes and queries are actually implemented as plugins under the hood. Some open-source plugins also serve as nice examples, e.g., ingest-langdetect and read-only-rest.

Elastiknn follows roughly the same structure as any Elasticsearch plugin that provides new datatypes and new queries. For example, Elasticsearch’s support for Geo queries is implemented as a plugin with an analagous structure. Instead of datatypes like geo_point and geo_shape, Elastiknn has elastiknn_dense_float_vector and elastiknn_sparse_bool_vector. Instead of queries like geo_bounding_box and geo_distance, Elastiknn has elastiknn_nearest_neighbors.

The Elasticsearch plugin sources are compiled and packaged as a zip file (pretty much a JAR), to be installed by the elasticsearch-plugin CLI – see the Installation Docs.

Finally, Elasticsearch plugins need to be re-built and re-released for every minor release of Elasticsearch. This is because Elasticsearch only maintains backwards-compatibility at the HTTP API level. The Java internals usually have a few minor breaking changes for every release (code changes and dependency updates). This makes it difficult to backport bug-fixes and new features to older versions of the plugin. Elastiknn has so far taken the approach that bug-fixes and new features are released only for the latest version of Elasticsearch.⁴

Programming Languages

The Elastiknn implementation is about 60% Scala and 40% Java. Scala is a JVM-based language, so we can call Java code from Scala, call Scala code from Java (with some limitations), and release Scala and Java sources as a single JAR. Scala is generally a more expressive language, however its abstractions are not always free. So Java is used for all the CPU-bound LSH models and Lucene abstractions, and Scala everywhere else.⁵

Distance vs. Similarity

Elasticsearch requires non-negative scores, with higher scores indicating higher relevance.

Elastiknn supports five vector similarity functions (L1, L2, Cosine, Jaccard, and Hamming). Three of these are problematic with respect to this scoring requirement.

Specifically, L1 and L2 are generally defined as distance functions, rather than similarity functions, which means that higher relevance (i.e., lower distance) yields lower scores. Cosine similarity is defined over \([-1, 1]\), and we can’t have negative scores.

To work around this, Elastiknn applies simple transformations to produce L1, L2, and Cosine similarity in accordance with the Elasticsearch requirements. The exact transformations are documented on the API page.

Locality Sensitive Hashing Background

Before we look at Elastiknn’s specific implementations of LSH, we should cover some LSH basics. The notation is biased to expedite explanation with respect to Elastiknn. There are additional resources which provide a more thorough, generalized presentation.³

Hash Functions that Preserve Locality

The idea of Locality Sensitive Hashing is that we can approximate exact pairwise similarity of vectors by converting each vector into hashes (usually just integers), with the key property that the probability of two vectors having the same hash correlates to their exact similarity.

In other words, we define a hash function which preserves the locality of vectors.

Each similarity function uses a different hash function, but the general structure is identical:

take a vector as input and produce an integer hash as output

More formally, a hash function \(h\) for a \(d\)-dimensional real-valued vector \(v\) is specified:

\[h(v): \mathbb{R}^d \rightarrow \mathbb{N}\]

And for boolean-valued vectors:

\[h(v): \{\text{true}, \text{false}\}^d \rightarrow \mathbb{N}\]

Query Pattern

The query pattern for LSH is quite simple:

1. Hash the query vector.
2. Find the indexed vectors having the most hashes in common with the query vector. These are typically called the candidates.
3. Re-rank them by computing exact similarity of the query vector vs. each candidate.
4. Return the top re-ranked candidates.

The user determines the number of candidates as a query-time hyper-parameter. The number of candidates is generally larger than the number of results that will be returned, but much smaller than the total index. For example, to find 10 results from an index of 1 million vectors, we might reasonably find and re-rank 1000 candidates. Obviously, as the number of candidates increases, the results improve at the cost of query time.

Amplification (\(k\) and \(L\))

\(h(v)\) produces a single integer hash.

We generally need several of these values to generate enough collisions to retrieve results.

To account for this, we use a technique called amplification, which comes in two varieties: AND amplification and OR amplification. These amplification techniques give us levers to control the precision and recall of the retrieved results.

AND amplification is the process of concatenating several distinct hash functions \(h_j(v)\) to form a logical hash function \(g_i(v)\). The integer hyper-parameter \(k\) is generally used to specify the number of concatenated functions.

\[g_i(v) = \text{concat}(h_{i k}(v), h_{i k + 1}(v), h_{i k + 2}(v) \ldots, h_{i k + k - 1}(v))\]

This is called AND amplification because the \(h_j(v)\) hashes are AND-ed together to form \(g_i\). As \(k\) increases, the probability of collision decreases, which generally results in higher precision.

OR amplification is the related process of computing multiple logical hashes \(g_i\) for every vector. The integer hyper-parameter \(L\) is generally used to specify the number of logical hashes computed for every vector.

This is called OR amplification because the \(g_i(v)\) hashes are OR-ed in order to retrieve candidates for a query vector \(v\). Another way to think about this is that we simply have \(L\) distinct hash tables, and each one uses a logical hash \(g_i(v)\). As \(L\) increases, the probability of collision increases, which generally results in higher recall.

Once we have \(L\) hashes, they need to be indexed in a way that disambiguates the result of \(g_1(v)\) from \(g_2(v)\) and so on. To do this, we can include the value of \(i\) in the logical hash value:

\[g_i(v) = \text{concat}(\hspace{0.5cm}i\hspace{0.5cm}, h_{i k}(v), h_{i k + 1}(v), h_{i k + 2}(v) \ldots, h_{i k + k - 1}(v))\]

Finally, increased recall and precision are not free. The number of operations to hash a vector is a function of \(L \times k\). The number of hash-to-doc-ID entries stored in the inverted index is a function of \(L\).

To summarize:

• increasing \(L\) generally increases recall
• increasing \(k\) generally increases precision
• neither of these is free – we pay in CPU, memory, and storage

Multiprobe LSH

As described in the prior section, we can manipulate recall by adjusting \(L\), but this comes at the cost of additional storage.

One clever technique to address this is Multiprobe LSH.⁶

The idea is that we can store fewer hashes in the index and instead compute additional hashes at query time to increase the probability of retrieving relevant results.

This is analagous to query-time synonym expansion in standard text retrieval: if our query includes car, then we might also consider looking for auto and vehicle.

What are the synonyms of a hash? This depends on the similarity function, but, in short, they are the adjacent hash buckets. The original paper presenting Multiprobe LSH is specific to L2 distance, but there’s no inherent limitation to just this one distance.

To be clear, Multiprobe LSH doesn’t really eliminate cost. Rather, it simply shifts the cost from CPU, memory, and storage at indexing time to CPU and memory at query time. Depending on the application, this can be a worthwhile tradeoff.

A Concrete Example: L2 LSH

Let’s look at the LSH model for the L2 distance function.

L2 (i.e., Euclidean) distance for two \(n\)-dimensional vectors \(u\) and \(v\) is defined:

\[\text{dist}_{L2}(u, v) = \sqrt{\sum_{i=1}^n{(u_i - v_i)^2}}\]

The scoring convention in Elasticsearch is such that higher-relevance results have higher scores. To satisfy this convention, Elastiknn converts L2 distance into a similarity:

\[\text{sim}_{L2}(u, v) = \frac{1}{1 + \text{dist}_{L2}(u, v)}\]

Elastiknn uses the Stable Distributions method with multi-probe queries to approximate this similarity.^{7 6}

Intuitively, this method hashes a vector \(v\) as follows:

1. project (i.e., dot product) the vector onto a randomly-generated vector \(A_j\)
2. add a random offset \(B_j\) to the scalar from step 1
3. divide the resulting scalar by a width parameter \(w\)
4. floor the scalar to represent a discretized section (or bucket) of \(A_j\)

The process looks like this:

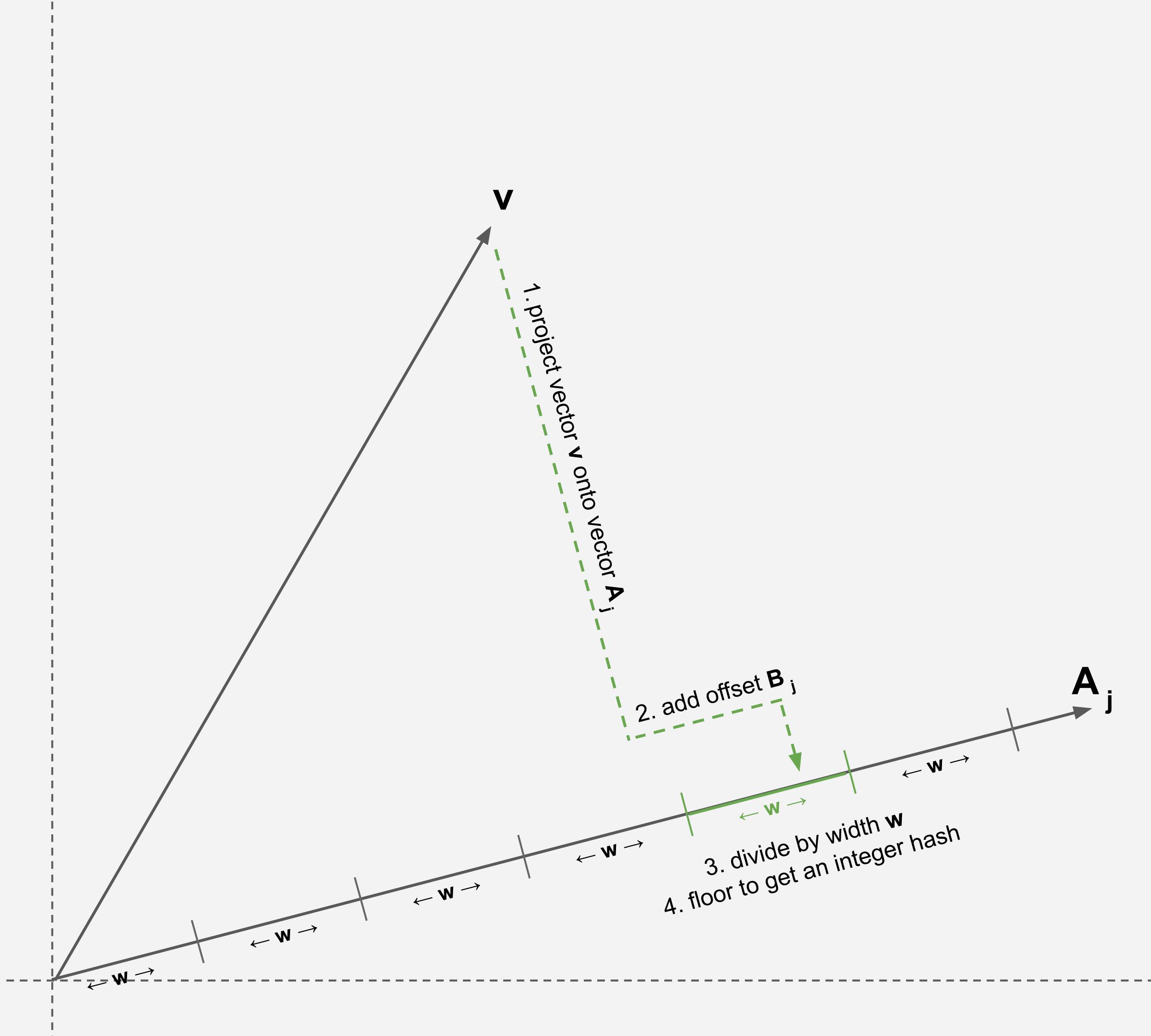
We can intuit that a vector close to \(v\) would be likely to hash to the same section of \(A_j\).

This hash function is defined more precisely as:

\[h_j(v) = \lfloor \frac{A_j \cdot v + B_j}{w} \rfloor\]

Each vector \(A_j\) is sampled from a standard Normal distribution and each scalar \(B_j\) is sampled from a uniform distribution in \([0, w]\).

The width \(w\) is provided as a hyper-parameter and depends on the magnitude of the vectors. As vector values increase, the scalar projections will increase, so \(w\) should also increase. If we think of hashing as putting vectors in buckets, then \(w\) is a bucket width.

We apply OR-amplification by computing \(L\) logical hash values, each of which is computed using AND-amplification. This is currently done as described in the above introduction for amplification: we concatenate the logical hash index (an integer in \([0, L)\)) with the \(k\) outputs from \(h_j(v)\) for \(j \in [0, k)\).⁸ We repeat this \(L\) times.

Multiprobe querying is a topic for another day. The short story is that we inject some logic into the function \(h_j(v)\) in order to perturb each of the \(k\) hashes. These perturbations generate the logical hashes adjacent to the actual logical hash, i.e., the hashes that are likely for nearby vectors. For more detail, see the original paper by Qin, et. al.,⁶ watch this lecture from IIT Kharagpur, or read the implementation on Github.⁹

Ok, let’s summarize.

The model hyper-parameters are:

• The bucket width parameter, \(w\)
• The number of tables for OR-amplification, \(L\)
• The number of hashes for AND-amplification, \(k\)

The actual model parameters are:

• \(L \times k\) random vectors \(A_j\) sampled from a standard Normal distribution
• \(L \times k\) random scalars \(B_j\) sampled from a uniform distribution over \([0, 1]\)

For every vector, we compute \(L \times k\) hashes and concatenate them into groups of size \(k\) to produce \(L\) logical hashes.

Locality Sensitive Hashing in Elastiknn

With this LSH background in mind, let’s look at how it’s actually implemented in Elastiknn.

Component Diagram

This diagram shows the components of Elastiknn and their interactions with Elasticsearch and Lucene.

The diagram is partitioned into rows and columns. The rows delineate three use-cases, from top to bottom: specifying a mapping that includes a vector, indexing a new document according to this mapping, and executing a nearest neighbor query against the indexed vectors. The columns delineate the systems involved, from left to right: the user, the Elasticsearch HTTP server, Elastiknn, and the Elasticsearch interface to Lucene.

The main takeaway from this diagram should be that Elastiknn has three responsibilities:

1. TypeParser parses a JSON mapping into a TypeMapper
2. TypeMapper converts a vector into Lucene fields, which are indexed by Lucene
3. KnnQueryBuilder converts the query vector into a Lucene query, executed by Lucene

Elasticsearch and Lucene handle everything else: serving requests, indexing documents, executing queries, and aggregating results.

Without further ado, behold the boxes and arrows:

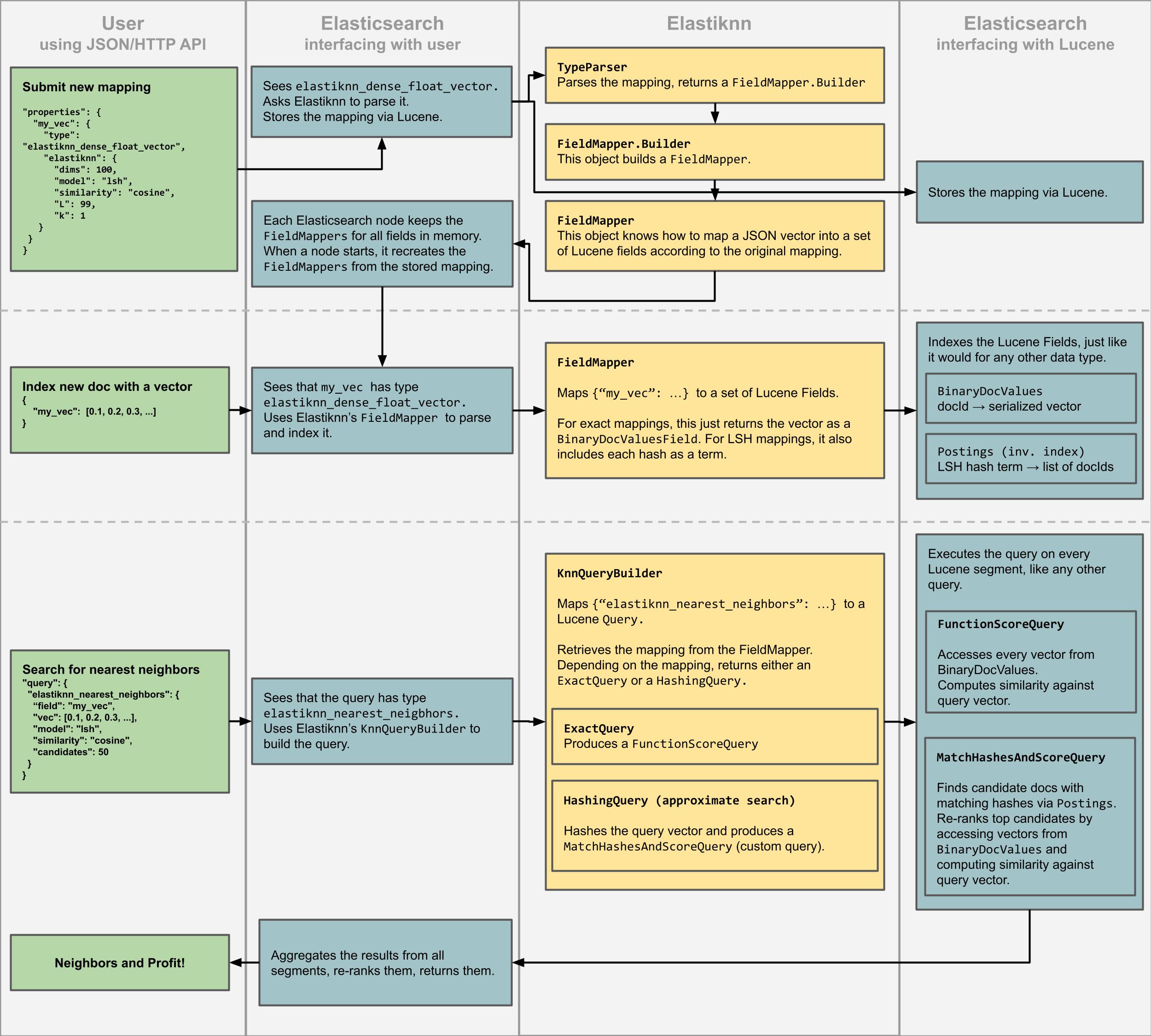
The most important and interesting parts of Elastiknn are the LSH models and the custom MatchHashesAndScoreQuery. The LSH models are used in the TypeMapper and KnnQueryBuilder to convert vectors into Lucene fields. The MatchHashesAndScoreQuery executes a simple, carefully-optimized term-based document retrieval and re-ranking. Both the models and custom query can be used independently of Elasticsearch, i.e., directly interfacing with Lucene.

Hashes are Just Words

The LSH paradigm is particularly compelling with respect to Lucene: we can store and search vector hashes just like words in a standard text document. In fact, there is virtually zero difference in how Lucene handles vector hashes compared to words. Both are serialized as byte arrays and used as keys in an inverted index.

The LSH models differ based on the similarity function they approximate, but they all share the same interface:

take a vector as input and produce a set of hashes as output.

The HashingModel interface, implemented by all LSH models, should convey this concisely.

Hashes can be repeated for some LSH models, so we represent them as a HashAndFreq type, which is just a container for a byte array and the frequency of occurrences. Hashing a vector produces an array of these HashAndFreq objects.

package com.klibisz.elastiknn.models;

public class HashingModel {
    public interface SparseBool {
        HashAndFreq[] hash(int[] trueIndices, int totalIndices);
    }
    public interface DenseFloat {
        HashAndFreq[] hash(float[] values);
    }
}

// A hash represented as a byte array and the frequency with which this hash occurred.
public class HashAndFreq implements Comparable<HashAndFreq> {
    public final byte[] hash;
    public final int freq;
    
    // Typical POJO boilerplate omitted.
}

Storage

Once the hashes are computed by a HashingModel, they have to be indexed. The vector also has to be stored, as we use it to compute exact similarity for the exact similarity models and when re-ranking the top approximate LSH candidates.

Each vector is serialized to a byte-array using the serialization utilities in sun.misc.Unsafe. This was found to be the fastest serialization abstraction for float arrays as of mid 2020.¹⁰ It’s then wrapped in an instance of BinaryDocValues and stored in Lucene’s column-oriented DocValues format. This is generally the largest part of an Elastiknn index, as it scales linearly with the number of vectors.

Each integer hash is serialized as a byte-array, also using sun.misc.Unsafe, although the performance benefits of using Unsafe are smaller here. It’s then wrapped in an instance of Field and stored in Lucene’s inverted-index Postings format. This part of the index scales with the product of the number of vectors, \(N\), and the number of hashes per vector, \(L\).

We expect somewhere between \(4L + 4NL\) bytes and \(8NL\) bytes of storage:

• \(4L + 4NL\) bytes assumes all vectors hash to exactly \(L\) hashes. \(4L\) bytes for integer hashes and \(4NL\) bytes for the integer doc IDs in the postings lists.
• \(8NL\) assumes all vectors hash to \(N\) unique hashes. \(4NL\) bytes for integer hashes and \(4NL\) bytes for integer doc IDs.

Both cases result in poor results and are very rare. The reality is somewhere in between.

Let’s do a back-of-envelope estimation for an index of 1 billion 128-dimensional floating-point vectors, each hashed to 100 hashes:

• 1 billion vectors times 128 dimensions times 4 bytes per float is 512 gigabytes
• 100 hashes times 4 bytes plus 1 billion vectors times 100 hashes times 4 bytes is 400 gigabytes and a rounding error.
• 1 billion vectors times 100 hashes times 8 bytes is 800 gigabytes.

So we need somewhere between 900 and 1300 gigabytes for this index. Keep in mind we can also decrease the number of hashes and use multiprobe hashing at query-time to trade-off storage and memory costs for CPU costs.

Finally, one might ask, “what about the LSH model parameters – you know, the random vectors and scalars – where are they stored?”

These parameters aren’t actually stored anywhere. Rather, they are lazily re-computed from a fixed random seed each time they are needed. The advantage of this is that it avoids storing and synchronizing large parameter blobs in the cluster. The disadvantage is that it’s expensive to re-compute the randomized parameters. Instead of re-computing them, we keep an LRU cache of models in each Elasticsearch node, keyed on the model type and its hyper-parameters.

Queries

We know how to hash and store the vectors. Now let’s look at how they’re queried.

As the component diagram indicated, we use the same LSH model to generate hashes for both indexing and querying. Once hashed, the query vector and its hashes are converted into a Lucene query and executed against each Lucene segment.

This query follows a relatively simple pattern. We just want to find the docs with the largest number of hashes in common with the query vector. Once we have them, we fetch their corresponding vectors in order to re-rank by exact similarity.

Let’s look at a couple ways to do this.

Simple but Slow: BooleanQuery

Lucene’s BooleanQuery is the simplest way to find the docs that share the largest number of hashes with the query vector.

The Scala code looks roughly like this:

val field = "myVec"
val hashes = Array(11, 22, 33, ...)
val builder = new BooleanQuery.Builder
hashes.foreach { h =>
  val term = new Term(field, new BytesRef(UnsafeSerialization.writeInt(h)))
  val termQuery = new TermQuery(term)
  val constQuery = new ConstantScoreQuery(termQuery)
  builder.add(new BooleanClause(constQuery, BooleanClause.Occur.SHOULD))
}
builder.setMinimumNumberShouldMatch(1)
val booleanQuery: BooleanQuery = builder.build()

We basically create a should occur clause for every hash and let Lucene find the docs that satisfy the largest number of clauses.

Unfortunately, this simple query proved to be a major bottleneck in Elastiknn LSH queries. Once vector serialization was optimized, some LSH queries were actually slower than exact queries, and the profiler indicated the system spending the majority of its time in this query and its related classes.

Here’s an excerpt from Github issue #76 from June 2020:

… I figured out that the biggest bottleneck for the various LSH methods is the speed of the Boolean Query used to retrieve vectors matching the hashes of a query vector. For example: on the ann-benchmarks NYT dataset (~300K 256d vectors), you can compute about 4.5 exact queries per second (with perfect recall). Once you switch to LSH, you can barely get over 2 queries per second with recall over 0.8. Most of that time is spent executing the boolean query. So you would have to get a dataset well into the millions to beat the exact search, and the breaking point is likely well over 1 second / query. …

Why is it so slow?

It’s a long story, but the summary is that the boolean query maintains state about its constituent term queries in order to optimize OR disjunctions. The cost of maintaining this state is negligible for queries with on the order of ten terms. This makes total sense, as a text search engine will rarely service queries longer than ten terms. However, LSH queries can easily have tens or hundreds of terms, and maintaining this state quickly becomes prohibitively expensive with that many terms.

Custom and Fast: MatchHashesAndScoreQuery

Based on the experimentation and recommendations of various Lucene community members on the mailing list,¹¹ it was determined that a custom Lucene query was justified for optimizing this query pattern.

Through several iterations, a custom query called MatchHashesAndScoreQuery was born.

The name is not particularly creative. This query takes some hashes and a scoring function, finds docs with the most matching hashes, and re-scores them using the scoring function.

The MatchHashesAndScoreQuerySuite shows some examples of its usage:

val hashes = Array(HashAndFreq.once(writeInt(42)), ...)
val q = new MatchHashesAndScoreQuery("vec", hashes, 10, indexReader,
  (_: LeafReaderContext) => 
    (docId: Int, numMatchingHashes: Int) => 
      (docId + numMatchingHashes) * 3.14f
)
val top10 = indexSearcher.search(q, 10)

This query is largely based on Lucene’s TermsInSetQuery. It mostly removes unnecessary functionality from that query, adds the ability to count exactly how many times each document matched any of the terms, and adds support for the scoring function.

To compare with the BooleanQuery approach: the BooleanQuery was barely able to exceed 2 single-threaded queries/second with 80% recall@100 on a dataset of 300k vectors. The MatchHashesAndScoreQuery exceeds 50 single-threaded queries/second with 80% recall@100 on a dataset of 1M vectors. So it’s more than a 25x speedup.

There is definitely still some room for improvement. For those interested, there are two open issues closely related to this topic:

• Github issue #160: Optimize top-k counting for approximate queries
• Github issue #156: More efficient counter for query hits

A couple shout-outs are in order: the article “Build your own custom Lucene query and Scorer” from OpenSource Connections was extremely helpful in building the custom Lucene query. Mike McCandless and other Lucene developers contributed instrumental advice on the mailing list and various issue trackers.

Open Questions

Performance

Performance improvements remain a priority. On single-threaded benchmarks, Elastiknn is an order-of-magnitude slower than some purpose-built vector search solutions.

To some extent there is an insurmountable cost compared to implementations closer to bare metal with in-memory indexing. Elastiknn runs on the JVM, where number crunching is generally slower and where vector-optimized instructions are not available. Elastiknn also uses Lucene, a disk-first indexing solution. Still, there is absolutely room to improve.

See the issues tagged performance for some interesting problems.

Support for range queries

Range queries, i.e., “return the neighbors within distance d” remain unimplemented. It’s an interesting problem to solve with hashing methods, as it requires expressing distance in terms of hashes and essentially computing a ball of hashes around the query vector.

See Github issue 279: Support for range queries (neighbors within some distance).

Data-Dependent LSH and Vector Preprocessing

Elastiknn’s hashing parameters (e.g., \(A\) and \(B\) in L2 LSH) are currently totally ignorant of the dataset. It’s likely that some amount of parameter fitting to the indexed dataset would improve results. How much fitting, and how to do it remain interesting questions. Elastiknn very intentionally supports incremental indexing. Parameter-fitting requires providing a representative chunk of data up-front, which is antithetical to the incremental implementation.

A related improvement might involve vector preprocessing. Can we recommend a simple vector preprocessing step that guarantees better results? For example, perhaps we can center the vectors (by subtracting the mean and dividing by the standard deviation along each dimension), thereby leading to more uniformly-distributed hash assignments.

Better Tooling for Finding Hyper-parameters

By far the most common question about Elastiknn is along the lines of “I tried this model with these parameters. Why are the results bad?”

This is generally extremely difficult to reproduce. The search results change depending on the Elasticsearch cluster and index configurations and the amount of data, so a small sample is insufficient. The data is often proprietary anyways.

Part of the solution is documenting the tradeoffs of hyper-parameters. Another part is building some new tooling to analyze Elasticsearch and Lucene indices to diagnose common pathologies, e.g., an index where a large majority of vectors are hashed to a very small number of unique hashes.

Conclusion

Hopefully this article has demystified some magic behind Elastiknn and leads to discussion and continued improvements in the project. To start the discussion, you can find me on Twitter @alexklibisz, or start a new discussion on the Elastiknn Github project.

---

1. For a brief introduction to vector search aimed at Elastiknn users, start watching this presentation at 1m56s. For a more general introduction, see this Medium article about the Billion-Scale Approximate Nearest Neighbor Search Challenge. ↩

2. The short story about Elasticsearch and Lucene: Lucene is a search library implemented in Java, generally intended for text search. You give Lucene some documents, and it parses the terms and stores an inverted index. You give it some terms, and it uses the inverted index to tell you which documents contain those terms. Elasticsearch is basically a distributed cluster of Lucene indices with a JSON-over-HTTP API. ↩

3. For a thorough textbook introduction to Locality Sensitive Hashing, including a bit of math, read Chapter 3 of Mining of Massive Datasets. For a thorough video lecture introduction, watch lectures 13 through 20 of the Scalable Data Science course from IIT Kharagpur. ↩ ↩²

4. The only alternative to Elastiknn’s release pattern seems to be maintaining a separate copy of the code for every version of Elasticsearch. This seems to be the approach taken by read-only-rest. ↩

5. To support the claim of Scala being more expressive, consider the difference between representing different query types as Scala case classes vs. Java POJOs. When deciding to use Java or Scala, I find it useful to ask if I’m optimizing “in the large” or “in the small.” For more context, see Daniel Spiewak’s post Why are Fibers Fast?. ↩

6. Multi-Probe LSH: Efficient Indexing for High-Dimensional Similarity Search by Qin Lv, et. al., 2007 ↩ ↩² ↩³

7. Stable distributions, pseudorandom generators, embeddings, and data stream computation by Piotr Indyk, 2006 ↩

8. AND-amplification doesn’t necessarily have to be implemented as a concatenation. There’s an open ticket to explore using an ordered hashing function like MurmurHash to condense the outputs to a single integer. ↩

9. Implementing the multiprobe algorithm and seeing it actually work was an extremely satisfying moment. ↩

10. The sun.misc.Unsafe utilities were carefully benchmarked as the fastest way to store a vector. Serialization is an area of the JVM where the performance of different abstractions varies wildly. Still, it’s not great that we use them. There’s an open issue for considering some alternatives. ↩

11. Lucene Java-user mailing list: Optimizing a boolean query for 100s of term clauses, June 23, 2020 ↩